Progressive Distillation for Fast Sampling of Diffusion Models
marii
A Quick Overview
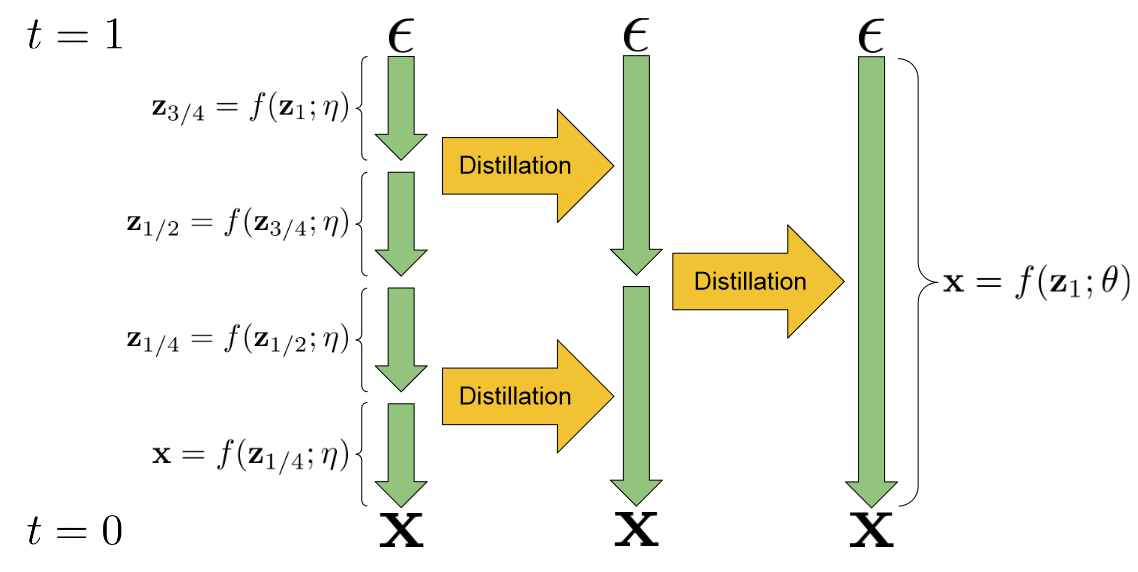
progressive_distillation.png
\(\tilde x\) is our target
- We take two steps of DDIM
- Then \(\tilde x\) is the image associated with taking two steps.
- The target of our distilled model is the output of our original diffusion model taking two ddim steps.
- We will cover \(w()\) later

Questions so far?
Why is \(\tilde x\) our target, and not \(\epsilon\)?
Break down of relationship between x and \(\epsilon\)
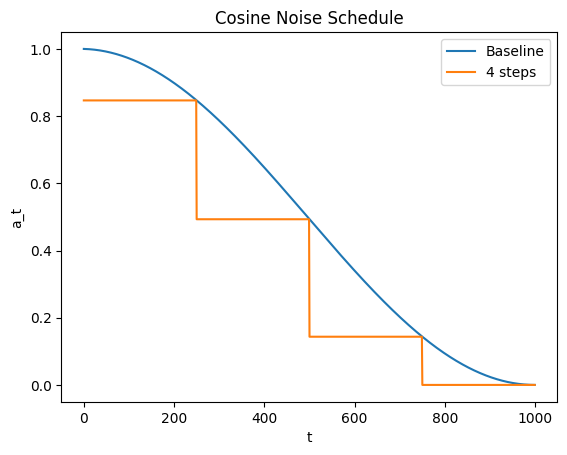
In the case of a single timestep \(||\epsilon_\theta(x_T)-\epsilon||^2_2\), could be optimized by an identity, and is not particularly useful. As our number of steps decreases to 4, this step becomes 1/4 of our total steps. (\(a_T\simeq0\))
\(\hat{x}_\theta(z_t) = \frac{1}{\alpha_t}(z_t-\sigma_t\hat{\epsilon}_\theta(z_t))\)
Our Options:
- Just predict \(x\) directly.
- Predict \(x\) and \(\epsilon\)
- Predict \(v = \alpha_t\epsilon+ \sigma x\)
\(w\)() is 0!
\(w()\) is 0, or very close to 0 near 0 and T. This problem becomes more aparent when we decrease the number of steps to 4. Our weights \(w\) becomes almost 0 for one of our 4 steps!
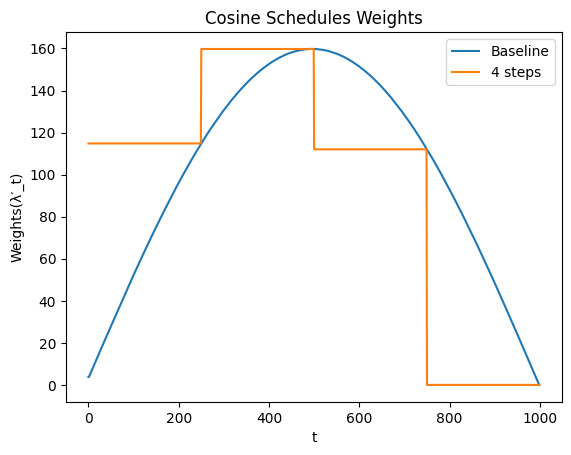
Alternative Weights
\(L_\theta = max(\frac{\alpha_t^2}{\sigma_t^2},1)||\hat x-x_t ||_2^2\) ‘truncated SNR weighting’
\(L_\theta=(1+\frac{\alpha_t^2}{\sigma_t^2})||\hat x-x_t ||_2^2\) ‘SNR+1 weighting’
I just clipped the weights.
Results
Notice the evaluations at powers of 2.
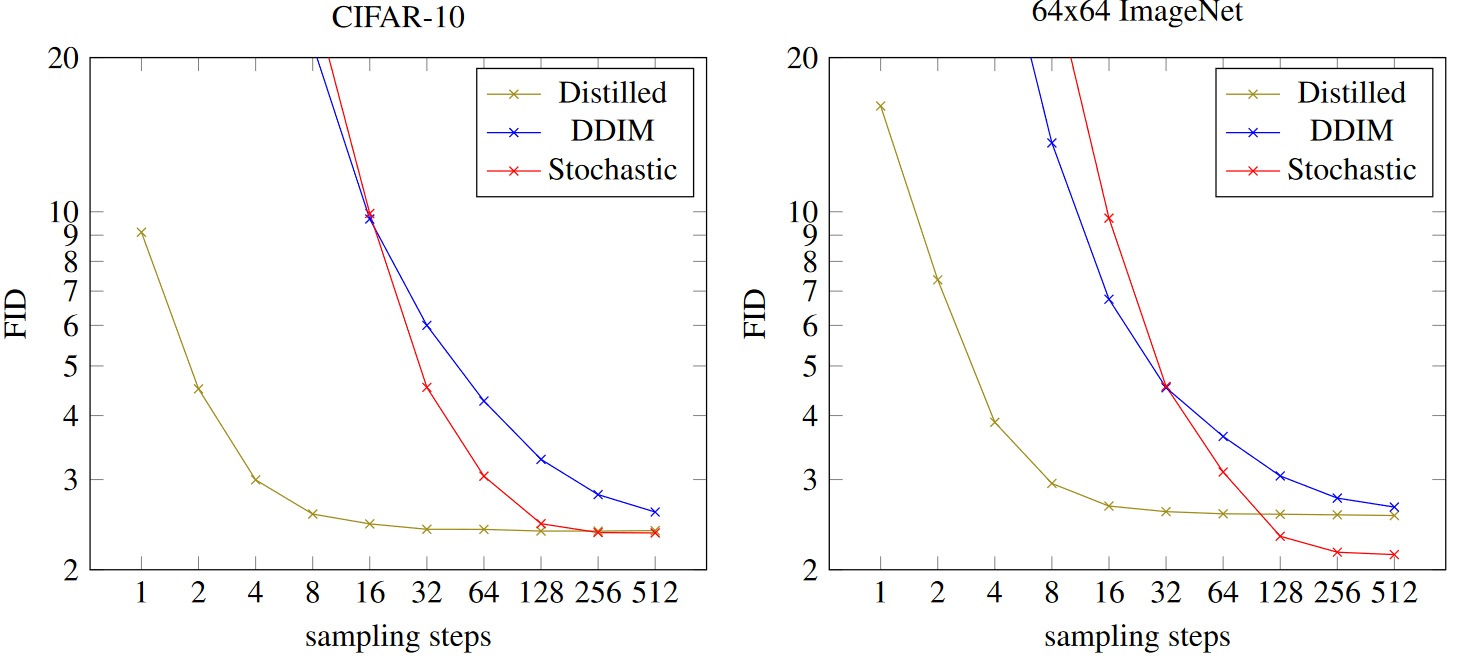
image.png
Derivation of the distillation target
from Appendix G
\(N\) : student sampling steps
\(t' = t-\frac{0.5}{N}\) : 1 teacher step, 1/2 student step
\(t'' = t-\frac{1}{N}\) : 2 teacher steps, 1 student step
We want to have 1 student step have input \(z_t\) and output \(\tilde{z}_{t''}\) equal to \(z_{t''}\)
\(\tilde{z}_{t''} = \alpha_{t''}\tilde{x}+\frac{\sigma_{t''}}{\sigma_t}(z_t-\alpha_t\tilde{x})=z_{t''}\)
\((\alpha_{t''}-\frac{\sigma_{t''}}{\sigma_t}\alpha_t)\tilde{x}+\frac{\sigma_{t''}}{\sigma_t}z_t=z_{t''}\)
\((\alpha_{t''}-\frac{\sigma_{t''}}{\sigma_t}\alpha_t)\tilde{x}=z_{t''}-\frac{\sigma_{t''}}{\sigma_t}z_t\)
\(\tilde{x}=\frac{z_{t''}-\frac{\sigma_{t''}}{\sigma_t}z_t}{(\alpha_{t''}-\frac{\sigma_{t''}}{\sigma_t}\alpha_t)}\)
Implmentation Notes
“We sample this discrete time such that the highest time index corresponds to a signal-to- noise ratio of zero, i.e. α1 = 0, which exactly matches the distribution of input noise z1 ∼ N (0, I) that is used at test time”
This is critical, I lost a lot of time on this one. I didn’t notice the problem until late in the process, so this might have actually been the cause for many other issues.
Cosine schedule seemed important for training model that predicts \(x\) instead of \(\epsilon\). Otherwise training unstable.
I did not succeed in using this technique on a parent model that predicts the noise. This may have been a bug, but training was a lot smoother with a parent that predicted \(x\) instead of \(\epsilon\).